
Will the Democratic candidate get at least this many electoral votes from these 7 swing states?
Basic
40
Ṁ3996resolved Nov 8
Resolved
YES 0
Resolved
NO 6
Resolved
NO10
Resolved
NO11
Resolved
NO15
Resolved
NO16
Resolved
NO17
Resolved
NO19
Resolved
NO21
Resolved
NO22
Resolved
NO25
Resolved
NO26
Resolved
NO27
Resolved
NO29
Resolved
NO30
Resolved
NO31
Resolved
NO32
Resolved
NO33
Resolved
NO34
Resolved
NO35
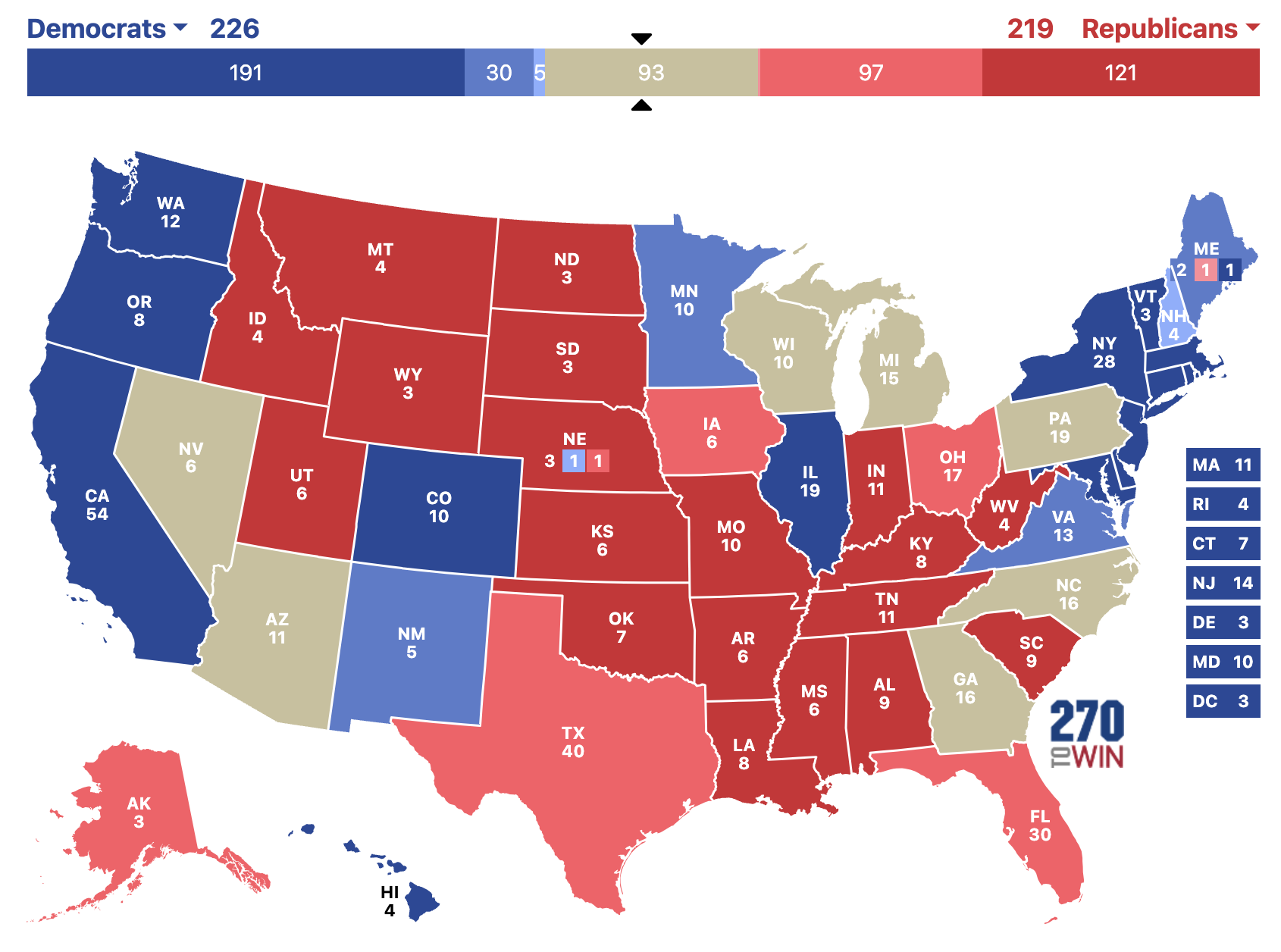
In the map below, seven states are marked as "Toss-up": Arizona, Georgia, Michigan, Nevada, North Carolina, Pennsylvania, and Wisconsin.
This question resolves YES for all numbers at and below the total number of electoral college votes among those states of these which the Democratic candidate wins.
Please provide answers in the form of whole numbers between 0 and 94. Other numbers are subject to N/A.
This question is managed and resolved by Manifold.
Get 1,000and
1,000and 3.00
3.00
Sort by:
@EvanDaniel A different market on the same set of states:
@EvanDaniel I originally made it as part of a network of markets for arbitrage of the top line POTUS outcome and state outcomes, but fees are higher now and I’m not sure how well it works for that anymore 🫤. One of these outcomes should still be pretty closely arbable with the big one.
Related questions
Related questions
Which keys will the Democratic Candidate win?
Close states: How many of 7 will vote Dem in 2024? AZ, GA, MI, NC, NV, PA, WI
Who will win at least one state in the 2028 Democratic Party presidential primaries?
How many electoral college votes will the Democratic Party nominee get in 2024? (Cumulative Market)
Will the Democratic presidential candidate receive an even number of electoral votes in the 2024 election?
90% chance
Will the winner of the 2024 US Presidential Election win at least 300 Electoral Votes?
98% chance
Will a Democrat have the Electoral College advantage in any of the next three elections (2024, 2028, or 2032)?
68% chance
Will any US Presidential candidate get more than 97% of the electoral vote by 2100?
22% chance